Problem 257: If ![]() , find the inverse function.
, find the inverse function.
Solution: We let ![]() .
.
![]()
Interchange ![]() and
and ![]() .
.
![]()
Solve for ![]() .
.
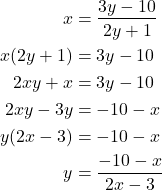
The new ![]() we call it
we call it ![]() . That is,
. That is,
![]()

Problem 257: If ![]() , find the inverse function.
, find the inverse function.
Solution: We let ![]() .
.
![]()
Interchange ![]() and
and ![]() .
.
![]()
Solve for ![]() .
.
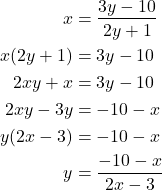
The new ![]() we call it
we call it ![]() . That is,
. That is,
![]()
Leave a Reply