Applications: Approximation of Area II

Problem 248: The area $A$ of the region $S$ that lies under the graph of the continuous function $f$ is the limit of the sum of the areas of approximating rectangles.

(1) $\begin{equation*} A = \lim_{n \to \infty} R_n = \lim_{x \to \infty} [f(x_1) \Delta x + f(x_2) \Delta x + \cdots + f(x_n) \Delta x]. \end{equation*}$

Use the above definition to determine the expression that represents the area under the graph of $f(x) = x^3$ from $x = 0$ to $x=1$ , and evaluate the limit. That is, the Riemann sum is given by

(2) $\begin{align*} R_n = \sum_{i=1}^{n} f(x_i) \Delta x. \end{align*}$

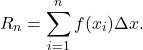
Since we are using rectangles of equal width,

(3) $\begin{equation*} \Delta x = \frac{b-a}{n} =\frac{1-0}{n} = \frac{1}{n}. \end{equation*}$

Thus (2) takes the following form:

(4) $\begin{equation*} R_n = \sum_{i=1}^{n} f(x_i) \Delta x = \sum_{i=1}^{n} f(x_i) \cdot \frac{1}{n}.\end{equation*}$

One can now find the $x_i$ . That is,

(5) $\begin{equation*} x_i = a + \Delta x \cdot i = 0 + \frac{1}{n} \cdot i = \frac{i}{n}. \end{equation*}$

One can now find the limit.

(6) $\begin{align*} A & = \lim_{n \to \infty} R_n \\ & = \lim_{x \to \infty} \sum_{i=1}^{n} f\left(\frac{i}{n}\right) \cdot \frac{1}{n} \\ & = \lim_{x \to \infty} \sum_{i=1}^{n} \left( \frac{i}{n}\right)^3 \cdot \frac{1}{n} \\ & = \lim_{x \to \infty} \frac{1}{n^4} \underbrace{\sum_{i=1}^{n} i^3}_{= \left( \frac{n(n+1)}{2}\right)^2} \\ & = \lim_{x \to \infty} \frac{1}{n^4} \cdot \frac{n^2(n+1)^2}{4} \\ & = \frac{1}{4}. \end{align*}$

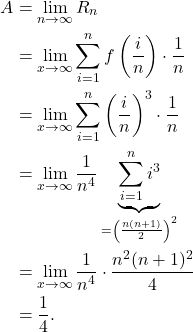
That is, the area is

(7) $\begin{equation*} A = \frac{1}{4}. \end{equation*}$

One Problem at a Time

Applications: Approximation of Area II

Leave a Reply Cancel reply