Problem 247: Consider the integral
(1) ![]()
(a) Find the Riemann sum for this integral using right endpoints and ![]() .
.
(b) Find the Riemann sum for this same integral, using left endpoints and ![]() .
.
Solution: The Riemann sum is given by
(2) ![]()
where ![]() is the number of triangles we use and
is the number of triangles we use and ![]() is the size of the width of the rectangles.
is the size of the width of the rectangles.
(a) In this case, ![]() . Since we are using rectangles with the same size, we have
. Since we are using rectangles with the same size, we have
(3) ![]()
Using (1), we have
(4) 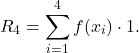
The only thing we are missing now is the ![]() . Since we are using right endpoints, we will go from
. Since we are using right endpoints, we will go from ![]() to
to ![]() by a step of
by a step of ![]() . That is,
. That is, ![]() . Therefore,
. Therefore,
(5) 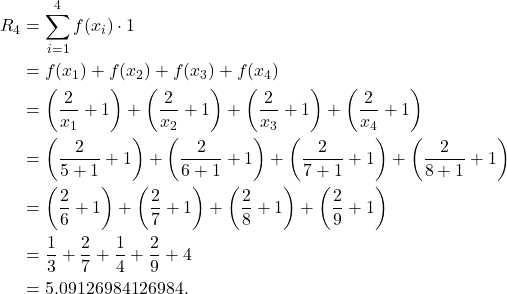
(b) In this case, the only thing that change is the ![]() since we are using left endpoints. We have
since we are using left endpoints. We have ![]() . That is,
. That is, ![]()
(6) 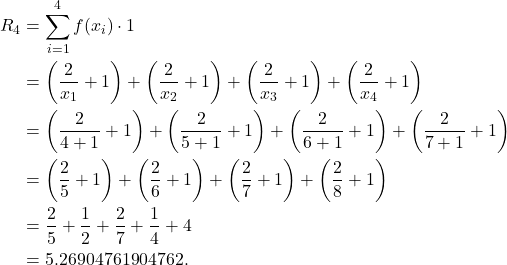

Leave a Reply