Problem 238: Show that
(1) ![]()
Solution: One can use integration by parts to show this. That is, let
(2) ![]()
and
(3) ![]()
Using the integration by parts formula,
(4) 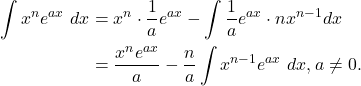
This completes the proof.
(5) ![]()

Problem 238: Show that
(1) ![]()
Solution: One can use integration by parts to show this. That is, let
(2) ![]()
and
(3) ![]()
Using the integration by parts formula,
(4) 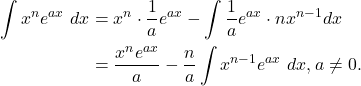
This completes the proof.
(5) ![]()
Leave a Reply