Problem 237: Show that
(1) ![]()
Solution: One can use integration by parts to show this. That is, let
(2) ![]()
and
(3) ![]()
By the integration by parts formula,
(4) 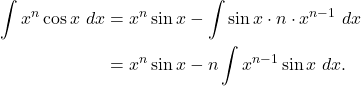
This shows what we wanted to show.
(5) ![]()

Problem 237: Show that
(1) ![]()
Solution: One can use integration by parts to show this. That is, let
(2) ![]()
and
(3) ![]()
By the integration by parts formula,
(4) 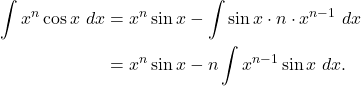
This shows what we wanted to show.
(5) ![]()
Leave a Reply