Problem 234: Evaluate the integral
(1) ![]()
Solution: First, we are going to use long division to rewrite our integral. That is, using long division,
(2) ![]()
One can now use this to rewrite our integral and integral. Thus,
(3) 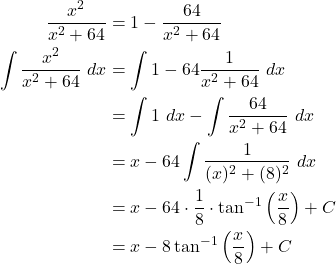
That is,
(4) ![]()

Problem 234: Evaluate the integral
(1) ![]()
Solution: First, we are going to use long division to rewrite our integral. That is, using long division,
(2) ![]()
One can now use this to rewrite our integral and integral. Thus,
(3) 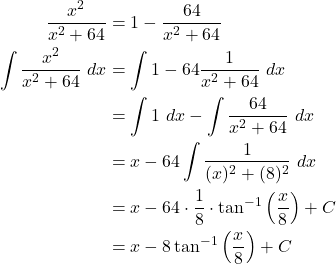
That is,
(4) ![]()
Leave a Reply