Problem 227: Consider the sequence ![]() .
.
a. What is the first term of the sequence?
b. What is the common ration?
c. What is the closed form for the ![]() term of the sequence?
term of the sequence? ![]()
d. Use the closed form to determine the value of ![]() .
.
Solution:
a. The first term is given by the first number in the sequence. Thus ![]() .
.
b. One can find the common ratio by dividing consecutive terms. That is,
(1) 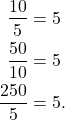
Thus the common ratio is 5.
c. Notice that ![]() . If you see the pattern, we can write it in general.
. If you see the pattern, we can write it in general.
(2) ![]()
d. Using (2), we can find ![]() .
.
(3) 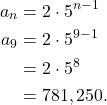

Leave a Reply