Problem 224: Consider the sequence ![]()
a. What is the common ration?
b. What are the next five terms in the sequence?
Solution: A geometric sequence is different from an arithmetic sequence. In an arithmetic sequence, we look for a common difference between the terms in the sequence whereas in the geometric sequence we look for a common ratio between the terms of the sequence.
a. Note that
(1) 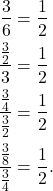
This means that the common ratio between the terms is ![]() .
.
b. Using the common ratios we can get the next five terms.
(2) 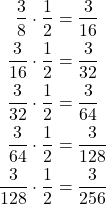

Leave a Reply