Problem 223: Consider the sequence ![]()
a. What is the common ration?
b. What are the next five terms in the sequence?
Solution: A geometric sequence is different from an arithmetic sequence. In an arithmetic sequence, we look for a common difference between the terms in the sequence whereas in the geometric sequence we look for a common ratio between the terms of the sequence.
a. Note that
(1) 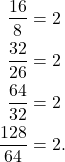
This means that the common ratio between the terms is 2.
b. Using the common ratios we can get the next five terms.
(2) 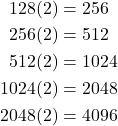

Leave a Reply