Problem 218: Factor the following polynomials completely:
(1) ![]()
Solution: In order to factor a quadratic polynomial, we need to identify the form of the polynomial. The polynomial is of the form ![]() where
where ![]() . The number in front of the squared term is bigger than 1. Thus we will use the “ac” method to factor the polynomial. The “ac” method consists of finding two number
. The number in front of the squared term is bigger than 1. Thus we will use the “ac” method to factor the polynomial. The “ac” method consists of finding two number ![]() and
and ![]() such that
such that
(2) ![]()
These two numbers are 14 and -1. Using the two found numbers we can rewrite the middle term of our polynomial and then factor by grouping.
(3) 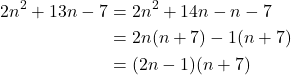
That is, ![]() .
.

Leave a Reply