3X3 System of Linear Equation

Problem 216: Solve

(1) $\begin{equation*} \begin{cases} x + 2y + 2z = 2 \\ -x + 2y + z = 5 \\ 5x + y + 5z = -4\end{cases}.\end{equation*}$

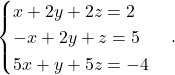
Solution: We can solve the system of linear equation in many ways. We will do it using matrix. That is,

(2) $\begin{equation*} \begin{cases} x + 2y + 2z = 2 \\ -x + 2y + z = 5 \\ 5x + y + 5z = -4\end{cases} \implies \underbrace{\begin{bmatrix}1 & 2 & 2 \\ -1 & 2 & 1 \\ 5 & 1 & 5 \end{bmatrix}}_{=A}\begin{bmatrix} x \\ y \\z \end{bmatrix} = \underbrace{\begin{bmatrix} 2 \\ 5 \\- 4\end{bmatrix}}_{=b}. \end{equation*}$

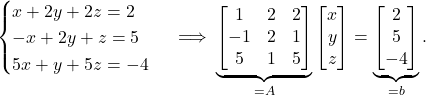
We can now write an augmented matrix using A and b. After using row operations we get

(3) $\begin{equation*} \begin{bmatrix} 1 & 2 & 2 \\ 0 & 4 & 3 \\ 0 & 0 & 7/4 \end{bmatrix} \begin{bmatrix} x \\ y \\z \end{bmatrix} = \begin{bmatrix} 2 \\ 7 \\ 7/4\end{bmatrix}.\end{equation*}$

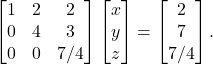
Going from bottom to the top we get

(4) $\begin{align*} x + 2y + 2z & = 2 \implies x + 2(1) + 2(1) = 2 \implies x = -2 \\ 4y + 3z & = 7 \implies 4y + 3(1) = 7 \implies y = 1 \\ \frac{7}{4}z & = \frac{7}{4} \implies z = 1. \end{align*}$

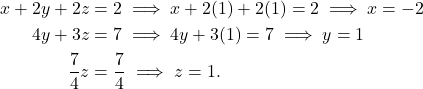
That is, the solution is given by $(-2,1,1)$ .

Leave a Reply Cancel reply