Problem 205: Solve the equation ![]() .
.
Solution: We will use arccosine to solve this problem. Notice that
(1) ![]()
since ![]() . This means that
. This means that
(2) ![]()
But these are not the only solutions. In general we have,
(3) 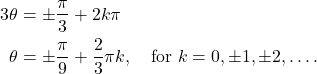
Hence,
(4) ![]()

Problem 205: Solve the equation ![]() .
.
Solution: We will use arccosine to solve this problem. Notice that
(1) ![]()
since ![]() . This means that
. This means that
(2) ![]()
But these are not the only solutions. In general we have,
(3) 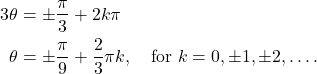
Hence,
(4) ![]()
Leave a Reply