Problem 201: Solve the system by using substitution: 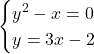
Solution: Using equation two and plugging it into equation one we have
(1) 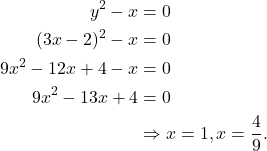
Using this ![]() ‘s values we can find the
‘s values we can find the ![]() ‘s values. That is,
‘s values. That is,
![]() :
:
(2) ![]()
![]() :
:
(3) ![]()
Thus the potential solutions are ![]() and
and ![]() . However, we need to check that this potential solutions satisfy the two equations. Hence,
. However, we need to check that this potential solutions satisfy the two equations. Hence,
![]() :
:
![Rendered by QuickLaTeX.com \[\begin{cases} y^2 -x = 0 \quad \Rightarrow \quad (1)^2 - 1 = 0 \\ y = 3x -2 \quad \Rightarrow \quad 1 = 3(1) - 2 \end{cases}\]](https://1problematatime.com/wp-content/ql-cache/quicklatex.com-2d0be6cfd2ec8945f500cd9485579654_l3.png)
Since the point ![]() does satisfies both equations, this point is a solution of the system.
does satisfies both equations, this point is a solution of the system.
![]() :
:
![Rendered by QuickLaTeX.com \[\begin{cases} y^2 - x = 0 \quad \Rightarrow \quad (-2/3)^2 - 4/9 = 0 \\ y = 3x - 2 \quad \Rightarrow \quad -2/3 = 3(4/9) - 2 \end{cases}\]](https://1problematatime.com/wp-content/ql-cache/quicklatex.com-6dc3d1bbb2e654b677a908141646cb22_l3.png)
Since the point ![]() does satisfies both equations, this point is a solution of the system.
does satisfies both equations, this point is a solution of the system.
Therefore, the system’s solutions are ![]() and
and ![]() .
.

Leave a Reply