Obtaining a Line from Two Points

Problem 198: Find the equation of a line that contains the points $(-4,-3)$ and $(1,-5)$ . Write the equation in slope-intercept form.

Solution: The slope-intercept form of a line is given by

(1) $\begin{equation*} y = mx + b.\end{equation*}$

Using our two given points we can the slope. That is,

(2) $\begin{align*} m & = \frac{y_2-y_1}{x_2 - x_1} \\ & = \frac{-5-(-3)}{1-(-4)} \\ & = \frac{-5+3}{1+4} \\ & = \frac{-2}{5}. \end{align*}$

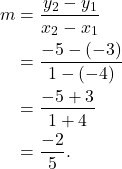
Then (1) takes the form

(3) $\begin{equation*} y = mx + b = -\frac{2}{5}x + b. \end{equation*}$

We just need to pick a point, from the two given, to find $b$ . That is, using $(1,-5)$

(4) $\begin{align*} y & = -\frac{2}{5}x + b \\ -5 & = - \frac{2}{5}(1) + b \\ -5 & = -\frac{2}{5} + b \\ 25 & = 2 + b \\ b & = 23.\end{align*}$

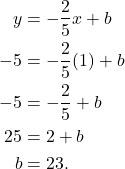
This complete our line.

(5) $\begin{equation*} y = -\frac{2}{5}x + 23 \end{equation*}$