Triangles Application

Problem 195: An architect is designing the entryway of a restaurant. She wants to put a triangular window above the doorway. Due to energy restrictions, the window can only have an area of 120 square feet and the architect wants the base to be 4 feet more than twice the height. Find the base and height of the window.

Solution: Since the architect wants to build a “triangular” window, we are dealing with a triangle here. The area of a triangle is given by

(1) $\begin{equation*} A = \frac{1}{2} \cdot b \cdot h, \end{equation*}$

where $b$ is the base and $h$ is the height of the triangle. Moreover, the architect wants the base of the triangle to be 4 feet more than twice the height. Thus $b = 2h + 4$ . Then

(2) $\begin{align*}A & = \frac{1}{2}b h \\ & = \frac{1}{2}(2h+4)h \\ & = h^2 + 2h. \end{align*}$

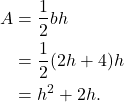
Since the area needs to be 120 square feet, we have

(3) $\begin{align*} A & = h^2 + 2h \\ 120 & = h^2 + 2h \\ h^2 + 2h - 120 & = 0 \\ (h + 12)(h-10) & = 0 \\ & \Rightarrow h = -12, 10. \end{align*}$

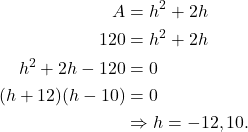
Since the height can’t be negative, the height of the triangle has to be 10 feet long. It follows that $b = 2(10) + 4 = 24$ feet long.

Hence, the triangle needs to have a base of 24 feet and height is 10 feet.

Leave a Reply Cancel reply