Right Triangle Application

Problem 194: A boat’s sail is in the shape of a right triangles. The hypothenuse will be 17 feet long. The length of one side will be 7 feet less than the length of the other side. Find the lengths of the other sides of the sail.

Solution: If we have a right triangle, we can use the Pythagoran Theorem to obtain an expression to work with. That is, let $x$ and $y$ be the length of the sides. Since the length of one side will be 7 feet less than the length of the other side, we have $y = x-7$ . Hence,

(1) $\begin{align*} 17^2 & = (x-7)^2 + x^2 \\289 & = x^2 - 14x + 49 + x^2 \\ 289 & = 2x^2 - 14x + 49 \\ 0 & = 2x^2 - 14x + 49 - 289 \\ 0 & = 2x^2 - 14x - 240 \\ 0 & = x^2 - 7x - 120 \\ 0 & = (x-15)(x+8) \\ & \Rightarrow x = 15, x = -8. \end{align*}$

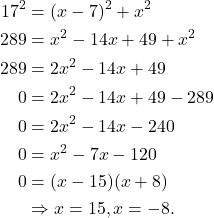
Since the length is nonnegative, we have $x = 15$ . Then $y = x - 7 = 15-7=8$ .

That is, the length of the sides is given by 15 feet and 8 feet.

Leave a Reply Cancel reply