Application of Area II

Problem 193: A rectangular patio has area 180 square feet. The width of the patio is three feet less than the length. Find the length and width of the patio.

Solution: We know that the area of a rectangle is given by

(1) $\begin{equation*} A = l \cdot w, \end{equation*}$

where $l$ is the length of the rectangle and $w$ is the width. Since the width of the patio is three feet less than the length, we have $w = l - 3$ . That is,

(2) $\begin{align*} A & = l \cdot w \\ 180 & = l \cdot (l-3) \\ 180 & = l^2 - 3l \\ 0 & = l^2 -3l - 180 \\ 0 & = (l-15)(l+12) \\ & \Rightarrow l = 15, l = -12. \\ \end{align*}$

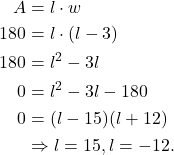
Since the length can’t be negative, we have $l = 15$ . Hence, $w = l - 3 = 15 - 3 = 12$ .

Therefore, the rectangle has length of 15 feet and width of 12 feet.

Leave a Reply Cancel reply