Problem 190: Solve the following differential equation given the initial condition:
(1) ![]()
Solution: In order to solve this problem, we need to find integrate both sides. That is,
(2) 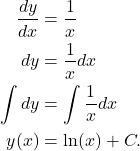
Using our initial condition, we can find ![]() . Thus
. Thus
(3) 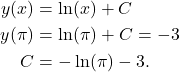
Hence,
(4) 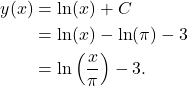

Leave a Reply