Problem 186: Find
(1) ![]()
Solution: First, we will find the integral by using the Fundamental Theorem of Calculus. Secondly, we will find the limit. That is,
(2) 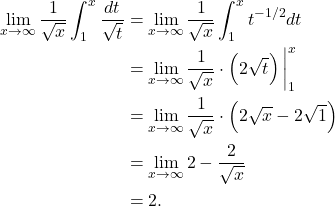
That is,
(3) ![]()

Problem 186: Find
(1) ![]()
Solution: First, we will find the integral by using the Fundamental Theorem of Calculus. Secondly, we will find the limit. That is,
(2) 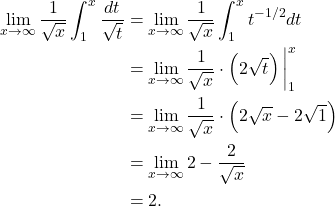
That is,
(3) ![]()
Leave a Reply