Problem 184: Verify that each of the two members ![]() satisfies the equation
satisfies the equation ![]() .
.
Solution: To verify the solution, we just need to plug in the solutions. That is,
If ![]() , then
, then
(1) 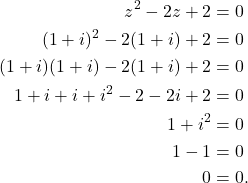
Likewise, if ![]() , then
, then
(2) 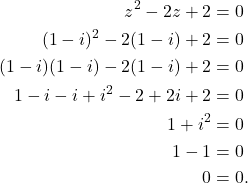
As desired, ![]() satisfies the equation
satisfies the equation ![]() .
.

Leave a Reply