Displacement of an Object

Problem 177: A rock is dropped from the top of a 400 foot cliff. Its velocity at time $t$ seconds is measured by $v(t)=-32t$ per second. Find the displacement of the rock during the time interval $2 \le t \le 4$ .

Solution: The displacement of the rock is given by the integral of the velocity function. That is,

(1) $\begin{align*} s(t) & = \int v(t) \ dt \\ & = \int_{2}^{4} v(t) \ dt \\ & = \int_{2}^{4} -32t \ dt \\ & = -\frac{32}{2}t^2 \bigg|_{2}^{4} \\ & = -16t^2\bigg|_{2}^{4} \\ & = -16(4)^2 + 16(2)^2 \\ & = -192. \end{align*}$

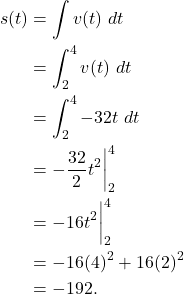
Therefore, the displacement of the rock is 192 feet during that time interval.

Leave a Reply Cancel reply