Problem 176: Use Newton’s Method to approximate the positive root of the equation
(1) ![]()
Solution: We know that the actual positive root of ![]() to 5-decimal places. We will use
to 5-decimal places. We will use
(2) ![]()
which is the Newton’s Method applied to our function ![]() .
.
We start with the guess ![]() . Then
. Then
(3) 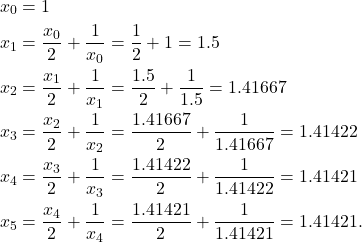
Note that we get an exact approximation to 5-decimal places after the 4th iterations.

Leave a Reply