Problem 157: Show that the number ![]() can be calculated as the limit
can be calculated as the limit
(1) ![]()
Solution: Let ![]() . Then
. Then ![]() at
at ![]() . But using the definition of derivative,
. But using the definition of derivative,
(2) 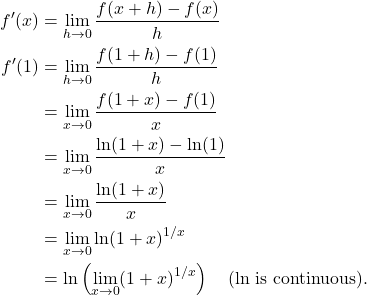
Because ![]() and
and ![]() is given by (2), they must be equal. That is,
is given by (2), they must be equal. That is,
(3) 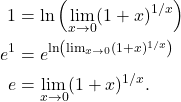
That is,
(4) ![]()

Problem 157: Show that the number ![]() can be calculated as the limit
can be calculated as the limit
(1) ![]()
Solution: Let ![]() . Then
. Then ![]() at
at ![]() . But using the definition of derivative,
. But using the definition of derivative,
(2) 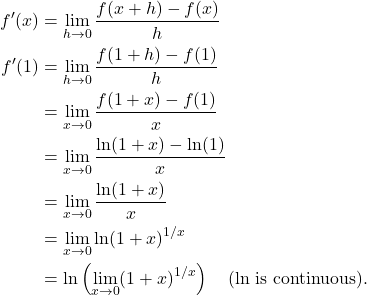
Because ![]() and
and ![]() is given by (2), they must be equal. That is,
is given by (2), they must be equal. That is,
(3) 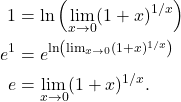
That is,
(4) ![]()
Leave a Reply