Linearly Independent Vectors

Problem 133: Determine if the following vectors are linearly independent.

(1) $\begin{equation*} \vec{\mathbf{v}_1} = [2,3-1], \quad \vec{\mathbf{v}_2} = [4,0,5], \quad \vec{\mathbf{v}_3} = [-2,15,-8]. \end{equation*}$

Solution: If the vectors in (1) are linearly independent, the equation

(2) $\begin{equation*} c_1 \cdot \vec{\mathbf{v}_1} + c_2 \cdot \vec{\mathbf{v}_2} + c_3 \cdot \vec{\mathbf{v}_3} = \vec{\mathbf{0}}\end{equation*}$

only has the trivial solution (i.e., $c_1=c_2=c_3=0$ ). On way we can identify this is by writing our vectors in an augmented matrix and reducing it to row reduced echelon form. That is,

(3) $\begin{equation*} \begin{bmatrix} 2 & 3 & -1 & | 0 \\ 4 & 0 & 5 & | 0 \\ -2 & 15 & -8 & | 0\end{bmatrix}. \end{equation*}$

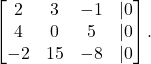
When we rows reduce this matrix (3), we get the following matrix

(4) $\begin{equation*} \begin{bmatrix} 1 & 0 & 0& | 0 \\ 0 & 1 & 0 & | 0 \\ 0 & 0 & 1 & | 0\end{bmatrix}. \end{equation*}$

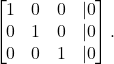
What does this mean? It means that there is no free variable. Hence, the only solution is the trivial solution. In other word, the only way to get the zero vector is if we take $c_1=c_2=c_3=0$ .

This means that the vectors in (1) are linearly independent.

Leave a Reply Cancel reply