Second Order ODE with Repeated Roots

Problem 128:

(a) Find the general solution to $y'' -12y' + 36y = 0.$

(b) Find the particular solution that satisfies $y(0) = 7$ and $y'(0) = 44$ .

Solution: The general solution of a second order ODE with repeated roots is given by

(1) $\begin{equation*} y(t) = c_1e^{r_1t} + c_2 t e^{r_2t}\end{equation*}$

where $r_1$ and $r_2$ are the roots of the characteristic polynomial.

(a) Let $y = e^{rt}$ so that $y' = re^{rt}$ and $y'' = r^2e^{rt}$ . This means that

(2) $\begin{align*} y'' -12y' + 36y & = 0 \\ r^2e^{rt} -12re^{rt} + 36e^{rt} & = 0 \\ r^2 - 12r + 36 & = 0 \\ (r-6)(r-6) & = 0 \\ & \Rightarrow r_1 = 6, r_2 = 6. \end{align*}$

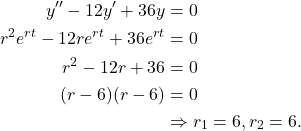
Hence, using (1), the general solution is given by

(3) $\begin{equation*} y(t) = c_1e^{6t} + c_2te^{6t}. \end{equation*}$

(b) Let’s now find the particular solution. First, we will find $c_1$ using the condition $y(0) = 7$ .

(4) $\begin{align*} c_1e^{6 \cdot 0} + c_2 \cdot 0 \cdot e^{6 \cdot 0} & = 7 \\ c_1 \cdot e^0 & = 7 \\ c_1 & = 7. \end{align*}$

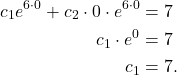
Then (3) takes the following form

(5) $\begin{equation*} y(t) = 7e^{6t} + c_2te^{6t} \quad \Rightarrow \quad y'(t) = 42e^{6t} + c_2e^{6t} + 6c_2te^{6t}.\end{equation*}$

Using our second condition, that is, $y'(0) = 44$

(6) $\begin{align*} \42e^{6\cdot 0} + c_2e^{6 \cdot 0} + 6c_2 \cdot 0 \cdot e^{6 \cdot 0} & = 44 \\ 42 + c_2 \cdot e^{0} & = 44 \\ 44 + c_2 & = 44 \\ c_2 & = 2. \end{align*}$

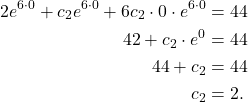
Therefore, the particular solution is given by

(7) $\begin{equation*} y(t) = 7e^{6t} + 2te^{6t}. \end{equation*}$

Leave a Reply Cancel reply