Problem 270: For the function
![]()
Find the ![]() – and
– and ![]() – intercepts.
– intercepts.
Solution: To find the ![]() intercept, we let
intercept, we let ![]() .
.
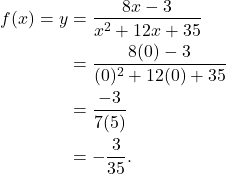
That is, the ![]() -intercept is
-intercept is ![]() .
.
To find the ![]() intercept, we let
intercept, we let ![]() .
.
![]()
Therefore, the ![]() -intercept is
-intercept is ![]() .
.

Problem 270: For the function
![]()
Find the ![]() – and
– and ![]() – intercepts.
– intercepts.
Solution: To find the ![]() intercept, we let
intercept, we let ![]() .
.
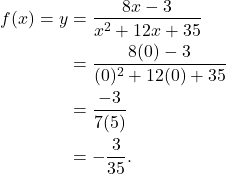
That is, the ![]() -intercept is
-intercept is ![]() .
.
To find the ![]() intercept, we let
intercept, we let ![]() .
.
![]()
Therefore, the ![]() -intercept is
-intercept is ![]() .
.
Leave a Reply