Problem 262: Given the polynomial
![]()
Solution: First, we need to rearrange the given polynomial from highest to smallest.
![]()
To find the possible roots of this polynomial we have to consider the possible factors of leading coefficient (call it ![]() ) and the constant coefficient (call it
) and the constant coefficient (call it ![]() ).
).
That is, the possible factors of 10 are: -10, -1, 1, 10, -2, -5, 2, 5.
The possible factors of -21 are: -1, 21, 1, -21, -7, 3,-3, 7.
The possible roots are given by
![]()
Simplifying, the possible roots are
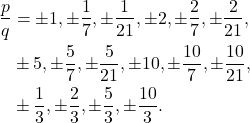

Leave a Reply