Problem 254: Consider ![]() . Calculate
. Calculate
![]()
Solution: One can compute the pieces of the quotient first and then put it all together.
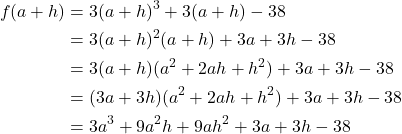
Putting it all together we have.
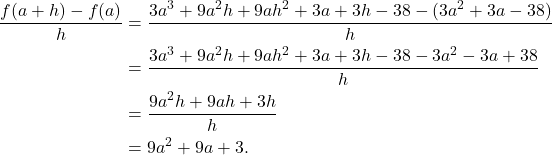

Problem 254: Consider ![]() . Calculate
. Calculate
![]()
Solution: One can compute the pieces of the quotient first and then put it all together.
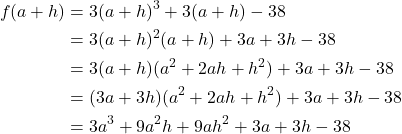
Putting it all together we have.
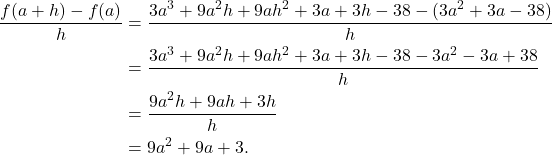
Leave a Reply