Radius of Converge of Series

Problem 250: The power series of $f(x)=e^x$ around $x = -2$ is given by

(1) $\begin{equation*} f(x) = \sum_{n=0}^{\infty} \frac{e^{-2}}{n}(x+2)^2 .\end{equation*}$

Find the radius of convergence.

Solution: One can use the ratio test to find the radius of convergence. That is, we an $L$ value such that

(2) $\begin{equation*} L = \lim_{n \to \infty} \frac{|a_{n+1}|}{|a_n|} < 1 \end{equation*}$

for all $x$ . Thus

(3) $\begin{align*} \lim_{n \to \infty} \frac{|a_{n+1}|}{|a_n|} & = \lim_{n \to \infty} \frac{|\frac{e^{-2}}{(n+1)!}(x+2)^{n+1}|}{|\frac{e^{-2}}{n!}(x+2)^n|} \\ & = \lim_{n \to \infty} \left( \frac{n!}{(n+1)!}\right)|x+2| \\ & = \lim_{n \to \infty} \left( \frac{1}{n+1}\right)|x+2| \\ & = 0 \cdot |x+2|. \end{align*}$

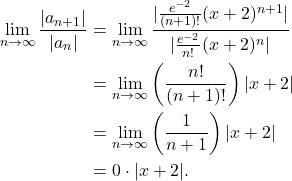
That is, we want

(4) $\begin{equation*} L = 0 \cdot |x+2| < 1, \end{equation*}$

which is true for all $x$ values. Therefore, the radius of convergence is $(-\infty, \infty)$ or $R = \infty$ .

Leave a Reply Cancel reply