Problem 239: Proof that
(1) ![]()
Solution: We will start by multiplying the numerator and denominator by the conjugate ![]() . That is,
. That is,
(2) 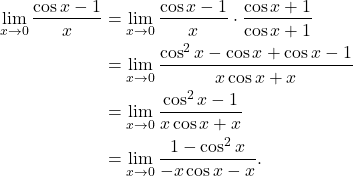
Let’s recall that ![]() so that
so that ![]() . Thus
. Thus
(3) 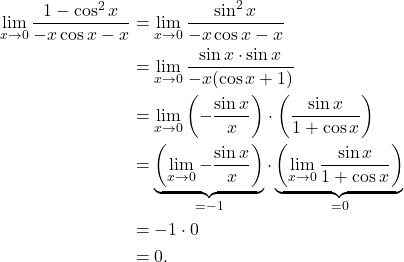
This completes the proof.

Problem 239: Proof that
(1) ![]()
Solution: We will start by multiplying the numerator and denominator by the conjugate ![]() . That is,
. That is,
(2) 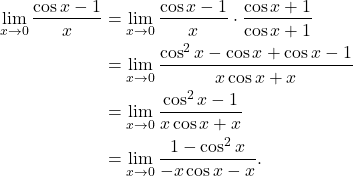
Let’s recall that ![]() so that
so that ![]() . Thus
. Thus
(3) 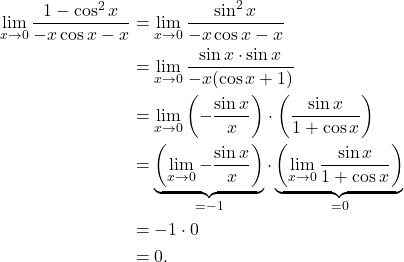
This completes the proof.
Leave a Reply