Problem 231: A traditional individual retirement account (IRA) is a special type of retirement account in which the money you invest is exempt from income taxes until you withdraw it. If you deposit $100 each month into an IRA earning 6% interest, how much will you have in the account after 20 years?
Solution: This type of accounts are called savings annuity. One can calculate the amount present in the annuity account with the following formula:
(1) 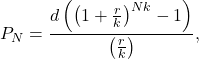
where ![]() is the balance in the account after N years,
is the balance in the account after N years, ![]() is the regular deposit (the amount you deposit each year, each month, etc.),
is the regular deposit (the amount you deposit each year, each month, etc.), ![]() is the annual interest rate in decimal form,
is the annual interest rate in decimal form, ![]() is the number of compounding periods in one year.
is the number of compounding periods in one year.
For our problem, we are looking for ![]() , and we are given
, and we are given ![]() and
and ![]() .
.
(2) 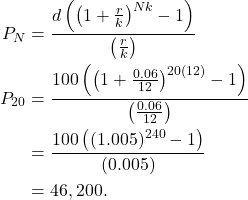
Thus, in 20 years you will have $46,200.

Leave a Reply