Problem 230: A landscape architect wished to enclose a rectangular garden on one side by a brick wall costing $40/ft and on the other three sides by a metal fence costing $20/ft. If the area of the garden is 182 square feet, find the dimensions of the garden that minimize the cost.
Solution: Let ![]() be the length of the brick wall and
be the length of the brick wall and ![]() be the length of an adjacent side with
be the length of an adjacent side with ![]() . The area is given by
. The area is given by
(1) ![]()
The cost if given by
(2) 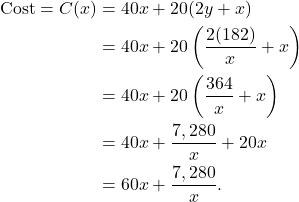
We now take the derivative and set it equal to zero to find critical points.
(3) 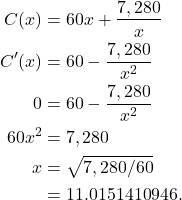
Using ![]() we can find
we can find ![]() .
.
(4) ![]()
Thus to minimize the cost we need ![]() length of the brick wall and
length of the brick wall and ![]() length of the adjacent side.
length of the adjacent side.

Leave a Reply