Problem 229: If you have 60 meters of fencing and want to enclose a rectangular area up against a long, straight wall, what is the largest area you can enclose?
Solution: The perimeter of a rectangle is given by
(1) ![]()
where ![]() is the length of the rectangle and
is the length of the rectangle and ![]() is the width of the rectangle. In this case, we are given one side already so that we don’t considered. The perimeter then take the form
is the width of the rectangle. In this case, we are given one side already so that we don’t considered. The perimeter then take the form
(2) ![]()
One can now find the area of the rectangle. That is,
(3) 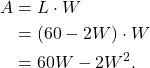
We now consider ![]() to find the critical point.
to find the critical point.
(4) 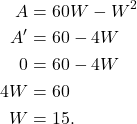
Using (2),
(5) ![]()
Notice that
(6) ![]()
By the second derivative test, we have an absolute maximum. Therefore, the largest area that can be enclosed is
(7) ![]()

Leave a Reply