Geometric Series

Problem 228: Find the requested sums:

$\sum_{n=1}^{13} \left( 2 \cdot 2^{n-1} \right)$

a. The first term appearing in this sum is?

b. The common ratio for our sequence is?

c. The sum is?

Solution: The general form of a geometric sequence is given by $a_n = a_1 \cdot r^{n-1}$ where $a_1$ is the first term of the sequence and $r$ is the common ratio of the sequence.

a. Notice that the given sequence is given in standard form.

(1) $\begin{equation*} \sum_{n=1}^{13} \left( 2 \cdot 2^{n-1} \right) \implies a_1 = 2, r = 2.\end{equation*}$

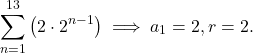
Therefore, the first term is $a_1 = 1$ .

b. Likewise from (a), the common ratio is $r = 2$ .

c. Using the first term and the common ratio we can find the sum. That is, the sum if given by

(2) $\begin{align*} a_n & = a_1 \left(\frac{1-r^n}{1-r} \right) \\ a_{13} & = 2 \cdot \left(\frac{1-2^{13}}{1-2} \right) \\ & = -2(1-2^{13}) \\ & = 16382.\end{align*}$

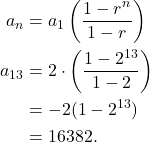
That is, the sum of the first 13 terms is 16382.

Leave a Reply Cancel reply