Derivatives and Tangent Lines

Problem 226: Let $f(x) = \sqrt{2x} + 1$ . Compute $f'(2)$ , the derivative of $f(x)$ at $x=2$ , and use the result to find an equation of the line tangent to the graph of $f$ at $(2,3)$ .

Solution: We will start by finding the derivative of $f(x)$ and then evaluate it at $x=2$ .

(1) $\begin{align*}f(x) & = \sqrt{2x} + 1\\ & = (2x)^{\frac{1}{2}} + 1 \\ f'(x) & = \frac{1}{2}(2x)^{-\frac{1}{2}} \cdot 2 \\ f'(x) & = \frac{1}{\sqrt{2x}} \\ f'(2) & = \frac{1}{\sqrt{2 \cdot 2}} \\ f'(2) & = \frac{1}{2}.\end{align*}$

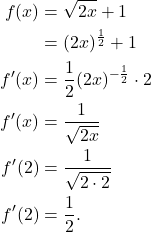
One can now find the tangent line using the found derivative (slope) and the point-slope formula of a line. Thus

(2) $\begin{align*} y-y_0 & = m(x-x_0) \\ y - 3 & = \frac{1}{2}(x-2) \\ y & = \frac{1}{2}x -1 + 3 \\ y & = \frac{1}{2}x + 2.\end{align*}$

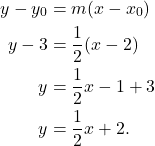
Therefore, the tangent line is given by $y = \frac{1}{2}x + 2$ .

Leave a Reply Cancel reply