End Behavior of Rational Functions

Problem 225: Use the limits at infinity to determine the end behavior of

(1) $\begin{equation*} f(x) = \frac{3x+2}{x^2 - 1}.\end{equation*}$

Solution: To determine the end behavior of a rational expression, we must take the limit at infinity of the function. That is,

(2) $\begin{align*} \lim_{x \to \infty} f(x) & = \lim_{x \to \infty} \frac{3x+2}{x^2 - 1} \\ & = \lim_{x \to \infty} \frac{\frac{3x}{x^2}+\frac{2}{x^2}}{\frac{x^2}{x^2}-\frac{1}{x^2}} \qquad \text{(Divide by higher power)} \\ & = \lim_{x \to \infty} \frac{\frac{3}{x} + \frac{1}{x^2}}{1-\frac{1}{x^2}} \\ & = \frac{0 + 0}{1-0}\\ & = \frac{0}{1} \\ & = 0.\end{align*}$

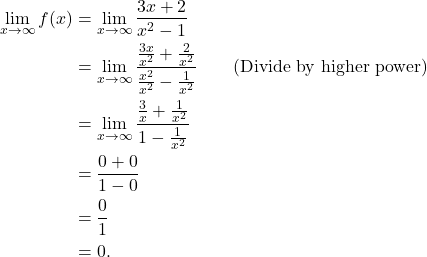
Thus $\lim_{x \to \infty} f(x) = 0$ . Likewise, $\lim_{x \to - \infty} f(x) = 0$ . This means that the function (1) has a horizontal asymptote at $y=0$ . Moreover, the vertical asymptotes are given by the zeros of the denominator.

(3) $\begin{align*} x^2 - 1 & = (x+1)(x-1) \implies x = -1, 1. \end{align*}$

Leave a Reply Cancel reply