Problem 221: Find the ![]() term in this sequence:
term in this sequence: ![]()
Solution: The ![]() term of an arithmetic sequence is given by
term of an arithmetic sequence is given by
(1) ![]()
where ![]() is the first term in the sequence and
is the first term in the sequence and ![]() is the common difference. To find the common difference, we just take the difference between the terms.
is the common difference. To find the common difference, we just take the difference between the terms.
(2) 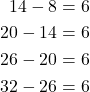
This means that ![]() . We are looking for
. We are looking for ![]() . That is,
. That is,
(3) 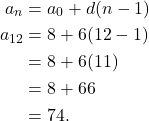
Thus ![]() .
.

Leave a Reply