Using Factoring to Simplify Rational Expressions

Problem 214: Simplify

(1) $\begin{equation*} \frac{x^2 - 16}{x^2 - 5x + 4}. \end{equation*}$

Solution: In order to simplify the rational expression, we need to factor the numerator and denominator. That is,

(2) $\begin{align*}\frac{x^2 - 16}{x^2 - 5x + 4} & = \frac{(x)^2 - (4)^2}{x^2 - 5x + 4} \end{align*}$

Notice that the numerator is a perfect square which we can factor easily. The denominator is quadratic equation with leading coefficient 1. Thus

(3) $\begin{align*}\frac{x^2 - 16}{x^2 - 5x + 4} & = \frac{(x)^2 - (4)^2}{x^2 - 5x + 4} \\ & = \frac{(x-4)(x+4)}{(x-4)(x-1)} \\ & = \frac{x+4}{x-2}.\end{align*}$

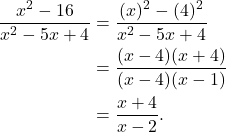
That is,

(4) $\begin{equation*} \frac{x^2 - 16}{x^2 - 5x + 4} = \frac{x+4}{x-2}.\end{equation*}$

One Problem at a Time

Using Factoring to Simplify Rational Expressions

Leave a Reply Cancel reply