Problem 213: Solve for ![]() :
:
(1) ![]()
Solution: We will start by factoring the denominators.
(2) ![]()
Now we get the denominator for the fractions so that we can add them. That is,
(3) 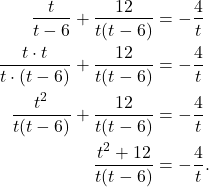
Now we can get rid of the denominator by multiplying both side by it.
(4) 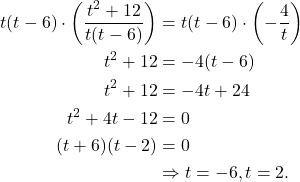
That is, ![]() and
and ![]() . The last step is to check that these are indeed the solutions by plugging in back the values. I will leave that to you!
. The last step is to check that these are indeed the solutions by plugging in back the values. I will leave that to you!

Leave a Reply