Problem 212: Solve for ![]() :
:
(1) ![]()
Solution: Let’s start with writing the term with constant coefficient.
(2) ![]()
One can now find a common denominator in order to add the two fractions. Also, we can multiply by ![]() both sides in order to simplify.
both sides in order to simplify.
(3) 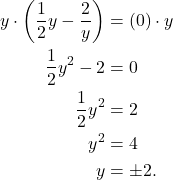
That is, ![]() . The last step is to check that this are indeed the solutions to the fractional equations. I will leave that step to you!
. The last step is to check that this are indeed the solutions to the fractional equations. I will leave that step to you!

Leave a Reply