Problem 206: Solve the equation ![]() .
.
Solution: We will use some trigonometric properties to solve this equation.
(1) 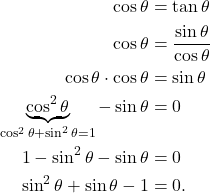
Notice that this is a quadratic equation. Let ![]() so that
so that
![]()
Using the quadratic equation we have
(2) ![]()
Thus ![]() or
or ![]() . However, -1.618 is not an option because this value is not in the unit circle. Therefore, we will only consider the
. However, -1.618 is not an option because this value is not in the unit circle. Therefore, we will only consider the ![]() . That is,
. That is,
(3) ![]()
There are two possible ![]() values that yield the y-coordinates 0.0618. Thus
values that yield the y-coordinates 0.0618. Thus
(4) 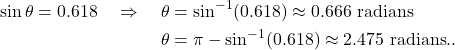

Leave a Reply