Problem 204: Solve the equation ![]() .
.
Solution: When solving trigonometric equation, we use the same method as solving algebraic equations i.e., solving for ![]() . Thus
. Thus
(1) 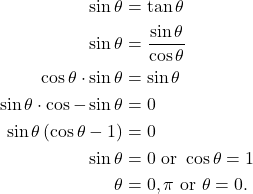
That is, ![]() . However, these are not the only solutions since any other multiple of
. However, these are not the only solutions since any other multiple of ![]() will also be a solution.
will also be a solution.
Hence,
![]()

Leave a Reply