Problem 203: Assume the orbit of Mercury around the sun is a perfect circle. Mercury is approximately 36 million miles from the sun.
- In one Earth day, Mercury completes 0.0114 of its total revolution. How many miles does it travel in one day.
- Use your answer from part (a) to determine the radian measure for Mercury’s moment in one Earth day.
Solution:
- Let’s begin by finding the circumference of Mercury’s orbit.
(1)
Since Mercury completes 0.0114 of its total revolution in one Earth day, we can now find the distance traveled: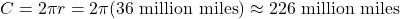
(2)
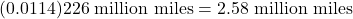
- Now, we convert to radians:
(3)

Leave a Reply