Problem 202: Suppose we are looking out a window that is 50 ft from the ground and we look down at a ![]() angle (this is called the angle of depression) to spot a fire on the ground. Approximately how far away from us in is the fire? Why is this only an approximation?
angle (this is called the angle of depression) to spot a fire on the ground. Approximately how far away from us in is the fire? Why is this only an approximation?
Solution: The angle between the person looking down the window and the high of the building is ![]() . Using this information, we can build a right-triangle where one of the side is the high of the building (50 feet) and the hypothenuse we will call it
. Using this information, we can build a right-triangle where one of the side is the high of the building (50 feet) and the hypothenuse we will call it ![]() which is what we are looking for. Then
which is what we are looking for. Then
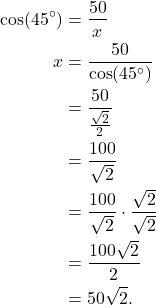
Hence, the fire is approximately ![]() feet away from us. This is only an approximation because we don’t know how fast the fire is spreading.
feet away from us. This is only an approximation because we don’t know how fast the fire is spreading.

Leave a Reply