Taking Limit of Riemann Sums

Problem 180: Find a formula for the Riemann sum obtained by dividing the interval $[a,b]$ into $n$ equal subintervals and using the right-hand endpoint for each $c_k$ . Then take a limit of these sums as $n \to \infty$ to calculate the area under the curve over $[a,b]$ .

$f(x) = x^2 + 1 \ \text{over the interval} \ [0,3]$

Solution: We will divide the interval $[0,3]$ into $n$ subintervals. Since the subintervals have the same length, the length of the subintervals is given by

$\Delta x = \frac{b-a}{n} = \frac{3-0}{n} = \frac{3}{n}.$

The height of the subintervals is given by

$f\left( \frac{3k}{n} \right), \quad k= 1,2,\dots, n,$

which is the height of the function at each right-hand point of the subintervals. That is, the Riemann sum is given by

(1) $\begin{align*} \sum_{k=1}^{n} f\left( \frac{3k}{n} \right) \cdot \Delta x & = \sum_{k=1}^{n} \left((3k/n)^2+1\right) \cdot \frac{3}{n} \\ & = \sum_{k=1}^{n} \frac{27k^2}{n^3} + \frac{3}{n} \\ & = \frac{27}{n^3} \cdot \underbrace{\sum_{k=1}^{n} k^2}_{= \frac{n(n+1)(2n+1)}{6}} + \frac{3}{n} \cdot \underbrace{\sum_{k=1}^{n}}_{= n} \\ & = \frac{27}{n^3} \cdot \left(\frac{n(n+1)(2n+1)}{6}\right) + 3 \\ & = \frac{27(2n^2+2n+1)}{6n^2} + 3.\end{align*}$

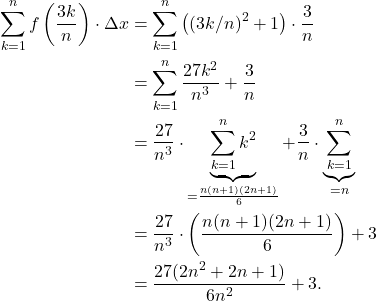
Taking the limit,

(2) $\begin{align*} \lim_{n \to \infty} \left( \frac{27(2n^2+2n+1)}{6n^2} + 3\right) & = \frac{27}{6} \cdot 2 + 3 \\ & = \frac{27}{3} + 3 \\ & = 9 + 3 = 12. \end{align*}$

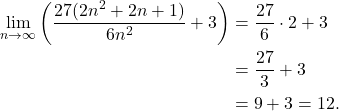
Hence, the area under the curve over the interval $[0,3]$ is $12$ .

Leave a Reply Cancel reply