Limit of Riemann Sums

Problem 179: Find a formula for the Riemann sum obtained by dividing the interval $[a,b]$ into $n$ equal subintervals and using the right-hand endpoint for each $c_k$ . Then take a limit of these sums as $n \to \infty$ to calculate the area under the curve over $[a,b]$ .

$f(x) = x + x^2 \ \text{over the interval} \ [0,1]$

Solution: We will divide the interval $[0,1]$ into $n$ subintervals. Since the subintervals have the same length, the length of the subintervals is given by

$\Delta x = \frac{b-a}{n} = \frac{1-0}{n} = \frac{1}{n}.$

The height of the subintervals is given by

$f\left( \frac{k}{n} \right), \quad k= 1,2,\dots, n,$

which is the height of the function at each right-hand point of the subintervals. That is, the Riemann sum is given by

(1) $\begin{align*} \sum_{k=1}^{n} f\left( \frac{k}{n} \right) \cdot \Delta x & = \sum_{k=1}^{n} \left( k/n+(k/n)^2\right) \cdot \frac{1}{n} \\ & = \sum_{k=1}^{n} \frac{k}{n^2} + \frac{k^2}{n^3} \\ & = \frac{1}{n^2} \cdot \underbrace{\sum_{k=1}^{n} k}_{= \frac{n(n+1)}{2}} + \frac{1}{n^3} \cdot \underbrace{\sum_{k=1}^{n} k^2}_{= \frac{n(n+1)(2n+1)}{6}} \\ & = \frac{1}{n^2} \cdot \left(\frac{n(n+1)}{2}\right) + \frac{1}{n^3} \cdot \left( \frac{n(n+1)(2n+1)} {6}\right) \\ & = \frac{n+1}{2n} + \frac{2n^2 + 3n + 1}{6n^2}.\end{align*}$

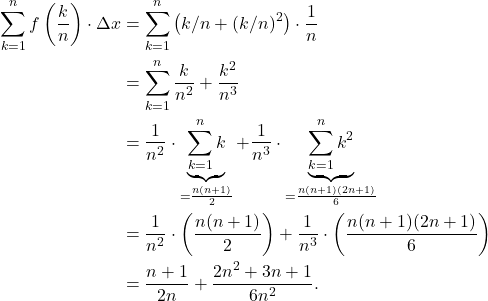
Taking the limit,

(2) $\begin{align*} \lim_{n \to \infty} \left( \frac{n+1}{2n} + \frac{2n^2 + 3n + 1}{6n^2}\right) & = \frac{1}{2} + \frac{2}{6} \\ & = \frac{10}{12} = \frac{5}{6}. \end{align*}$

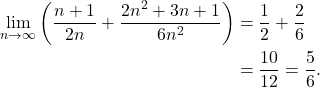
Hence, the area under the curve over the interval $[0,1]$ is $\frac{5}{6}$ .

Leave a Reply Cancel reply