Problem 175: Determine the concavity of the function ![]() on its domain.
on its domain.
Solution: The domain ![]() is given by
is given by ![]() . In order to find the concavity of a differentiable function, we use the second derivative. That is,
. In order to find the concavity of a differentiable function, we use the second derivative. That is,
(1) 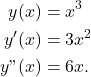
We have a change of concavity at the inflection point (that is, ![]() ). Then we have
). Then we have
![]()
Since ![]() on the interval
on the interval ![]() , the function
, the function ![]() is concave down on the interval
is concave down on the interval ![]() .
.
Likewise, since ![]() on the interval
on the interval ![]() , the function
, the function ![]() is concave up on the interval
is concave up on the interval ![]() .
.

Leave a Reply