Problem 173: A rectangle is to be inscribed in a semicircle of radius 2. What is the largest area the rectangle can have, and what are its dimensions?
Solution: Let ![]() be the coordinates of the corner of the rectangle obtained by placing the circle and rectangle in the coordinate plane. The length, height, and area of the rectangle can then be expressed in terms of the position
be the coordinates of the corner of the rectangle obtained by placing the circle and rectangle in the coordinate plane. The length, height, and area of the rectangle can then be expressed in terms of the position ![]() of the lower right-hand corner:
of the lower right-hand corner:
![]()
Notice that the values of ![]() are to be found in the interval
are to be found in the interval ![]() , where the selected corner of the rectangle lies. The goal is to find the absolute maximum value of the function
, where the selected corner of the rectangle lies. The goal is to find the absolute maximum value of the function
(1) ![]()
on the domain ![]() . Using the derivative to find the critical points,
. Using the derivative to find the critical points,
(2) 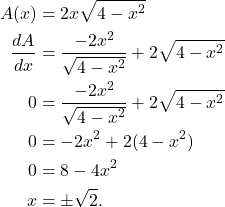
Only ![]() lies in the interior of the domain of
lies in the interior of the domain of ![]() . That is,
. That is,
(3) 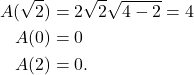
The area has a maximum value of 4 when the rectangle is ![]() units high and
units high and ![]() units long.
units long.

Leave a Reply