Problem 172: Find the amount of medicine to which the body is most sensitive by finding the value of ![]() that maximizes the derivative
that maximizes the derivative ![]() , when
, when
(1) ![]()
and ![]() is a constant.
is a constant.
Solution: We need to find the derivative with respect to ![]() twice. That is,
twice. That is,
(2) 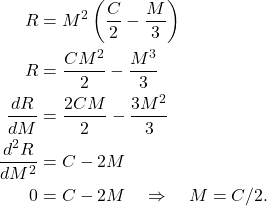
That is, by the Second Derivative Test, ![]() gives the maximum amount of medicine.
gives the maximum amount of medicine.

Leave a Reply