Derivatives in Business and Economics

Problem 171: It costs you $c$ dollars each to manufacture and distribute backpacks. If the backpacks sell at $x$ dollars each, the number sold is given by

(1) $\begin{equation*} n = \frac{a}{x-c} + b(100-x), \end{equation*}$

where $a$ and $b$ are positive constants. What selling price will bring a maximum profit?

Solution: In order to find the maximum profit, we need to find an equation for the profit. That is,

(2) $\begin{equation*} \text{Profit} = \text{Revenue} - \text{Cost}.\end{equation*}$

Let $P(x)$ be the profit so that

(3) $\begin{align*} P(x) & = nx - nc \\ & = n(x-c) \\ & = (x-c) \cdot \left(\frac{a}{x-c} + b(100-x) \right) \\ & = a + b(x-c)(100-x) \\ & = a + (bx-bc)(100-x). \end{align*}$

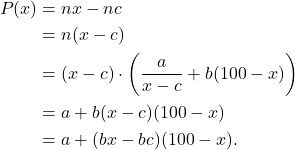
The maximum profit is given when $dP/dx=0$ . Hence,

(4) $\begin{align*} P(x) & = a + (bx-bc)(100-x) \\ \frac{dP}{dx} & =b(100-x) + (bx-bc)(-1) \\0 & = 100b - bx - bx + bc \\ 0 & = 100b + bc -2bx \\x & = \frac{-100b-bc}{-2b} \\ x & = 50 + \frac{c}{2}.\end{align*}$

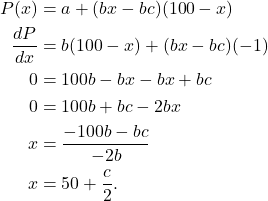
That is, the maximum profit is given when $x = 50 + \frac{c}{2}$ .

One Problem at a Time

Derivatives in Business and Economics

Leave a Reply Cancel reply